Python で数学と仲直り！これなら分かる最小二乗法と直線の当てはめ問題

どうしたの？なんかふるえてるけど。

いや…… ある日 LINE で遊んでいたら、相手の隠していた爪が露わになって戦慄しているのです。

高校最初のテストで世界トップクラスの成績……。

f:id:tercel_s:20200229200808j:plain:w350

……なんか、定期的にガチ勢ぜいに出会うよね。

文系だろうが理系だろうが 100点は 100点だし世界の頂点だし神。

おわかりいただけただろうか。

なんでキミがそんなに偉そうなんだよ！

まぁでも、たーせるくんも常つね々づね数学と仲直りしたがっているみたいだし、今日は軽く数学のお話でもしようか。

わーい。

数式だけだと退屈だから、後半ちょっとプログラミングもやろう。

参考文献

金谷健一著, 『これなら分かる応用数学教室―最小二乗法からウェーブレットまで』, 共立出版(2003).

直線の当てはめ

いいかい？

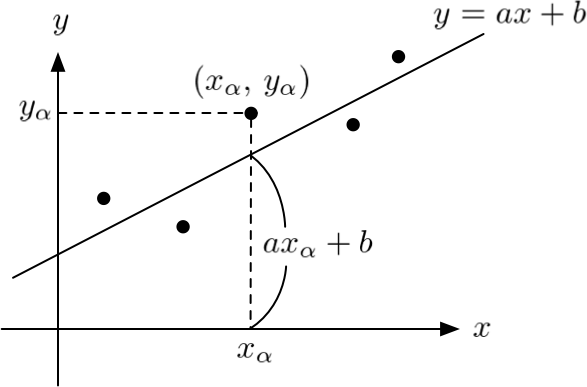
${N}$ 個のデータ ${(x_{1},\,y_{1}),\, \cdots ,\, (x_{N}, \, y_{N})}$ に直線を当てはめたいとしよう。

わくわく。

ここで、当てはめたい直線を ${y = ax + b}$ と置く。

${a,\, b}$ は、どちらもこれから求める未知の定数だよ。

f:id:tercel_s:20200229160415p:plain:w300

どう頑張っても、全ての点を通る直線って無理だよね。もんにょり。

そうだね。

だから、すべての点の一番近くを通る直線を見つけることにしよう。

がってん。

これは、 ${y_{\alpha } \approx ax_{\alpha} + b, \quad \alpha = 1, \, \cdots , \, N}$ を満たす $a,\,b$ を見つける問題と見なせる。

ただし、 $\approx$ は「ほぼ等しい」という意味。

なるほど。。。

各点の ↕︎ をできるだけ短くできればいいのか。

f:id:tercel_s:20200229163220p:plain:w300

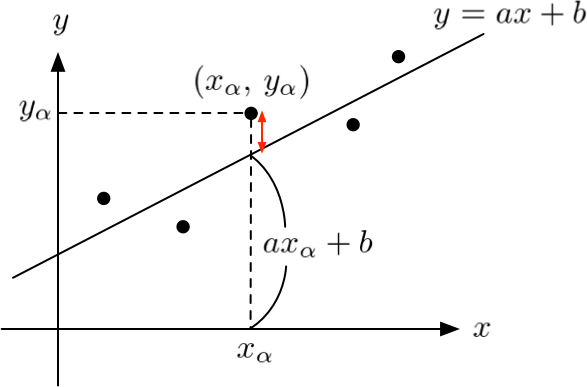
各点と直線のズレを最小にする問題を、以下のように解釈しよう。

ちなみに、 $\rightarrow \textrm{min}$ は、その左側の式を最小にすることを表すものとするよ。

${ J = \dfrac{\,1\,}{2} \displaystyle\sum_{\alpha = 1}^{N} \bigl\{ y_{\alpha } - \left( ax_{\alpha } + b \right) \bigr\}^{2} \rightarrow \textrm{min} }$

最初の $\frac{\,1\,}{2}$ という係数はどこから出てきたの……？

後の計算をラクにするためのおまじないだよ。

これで、変数 $a,\,b$ の2次関数の最小値を求めればよいことが分かるでしょ。

あ、なんか聞き覚えがあるぞ！

2次関数の最大値・最小値は、中学で平方完成を使った解法を学ぶので馴染みが深いと思う。

でも今回は多変数関数だから偏微分で解くよ。

あああああ（失禁

多変数関数が最大値や最小値をとる点では、各変数に関する偏導関数が 0 でなくてはならない。

厳密には例外もあるんだけど、ここでは微分できないような素性の悪い関数のことは考えないよ。

そういえば高校生の頃、関数 ${f(x)}$ の極きょく値ちを求めるために、 ${f'(x) = 0}$ を $x$ で解いたっけ。

あれは1変数関数だったけど、条件さえ揃えば多変数関数でも同じ議論が成立するんだったね。

従って、 ${ \dfrac{\partial J}{\partial a} = 0,\, \dfrac{\partial J}{\partial b} = 0}$ を解けば ${a,\, b}$ が求められる。

肩慣らしだ、やってみよう。

${ \begin{align} \dfrac{\, \partial J\,}{\partial a} &= \displaystyle \sum_{\alpha = 1}^{N} \left( y_{\alpha} - ax_{\alpha } - b \right) \left( -x_{\alpha} \right) \\ &= a \displaystyle \sum_{\alpha = 1}^{N} x_{\alpha}^{2} + b \displaystyle \sum_{\alpha = 1}^{N} x_{\alpha} - \displaystyle \sum_{\alpha = 1}^{N} x_{\alpha}y_{\alpha} \\ \dfrac{\, \partial J\,}{\partial b} &= \displaystyle \sum_{\alpha = 1}^{N} \left( y_{\alpha} - ax_{\alpha } - b \right) \left( -1 \right) \\ &= a \displaystyle \sum_{\alpha = 1}^{N} x_{\alpha} + b \displaystyle \sum_{\alpha = 1}^{N} 1 - \displaystyle \sum_{\alpha = 1}^{N} y_{\alpha} \end{align} }$

ちょっと待って！ いきなり何したの？

単なる合成関数の微分だよ。

${ y = f \left( g \left( x\right) \right) }$ のとき、 ${ y' = f' \! \left( g \left( x \right) \right) \! \cdot \! g' \! \left( x \right) }$ っていう公式、覚えてる？

いやまぁ…… それは覚えている。

ただ、なんか微分する際に $\sum$ をこんなふうに扱っていいのか一瞬わからなくなったんだ。

問題ないよ。

導関数の線せん型けい性といって、関数 $f(x),\, g(x)$ がともに微分可能ならば $\left\{ c f(x) \right\}' = c\! \cdot \! f'(x)$ が成り立つし（ $c$ は定数）、 ${ \left\{ f(x) \pm g(x) \right\}' = f'(x) \pm g'(x) }$ も成り立つよ。

この命題は微分の定義からほぼ明らかだよ。

ホントだ。

というか、邪悪な $\sum$ を解除して展開したら計算が合った。

結局、これを行列の形で書き直すと以下のようになる。

この方程式を解けば $a,\,b$ が定まるよ。

${ \begin{pmatrix} \displaystyle\sum_{\alpha = 1}^{N} x_{\alpha}^{2} & \displaystyle\sum_{\alpha = 1}^{N} x_{\alpha } \\ \displaystyle\sum_{\alpha = 1}^{N} x_{\alpha} & \displaystyle\sum_{\alpha = 1}^{N} 1 \end{pmatrix} \begin{pmatrix} a \\ b \end{pmatrix} = \begin{pmatrix} \displaystyle\sum_{\alpha = 1}^{N} x_{\alpha} y_{\alpha} \\ \displaystyle\sum_{\alpha = 1}^{N} y_{\alpha} \end{pmatrix} }$

ここからの計算量ヤバいじゃん。

こんなものどうやって解けと。

Python を使えば楽勝だよ。

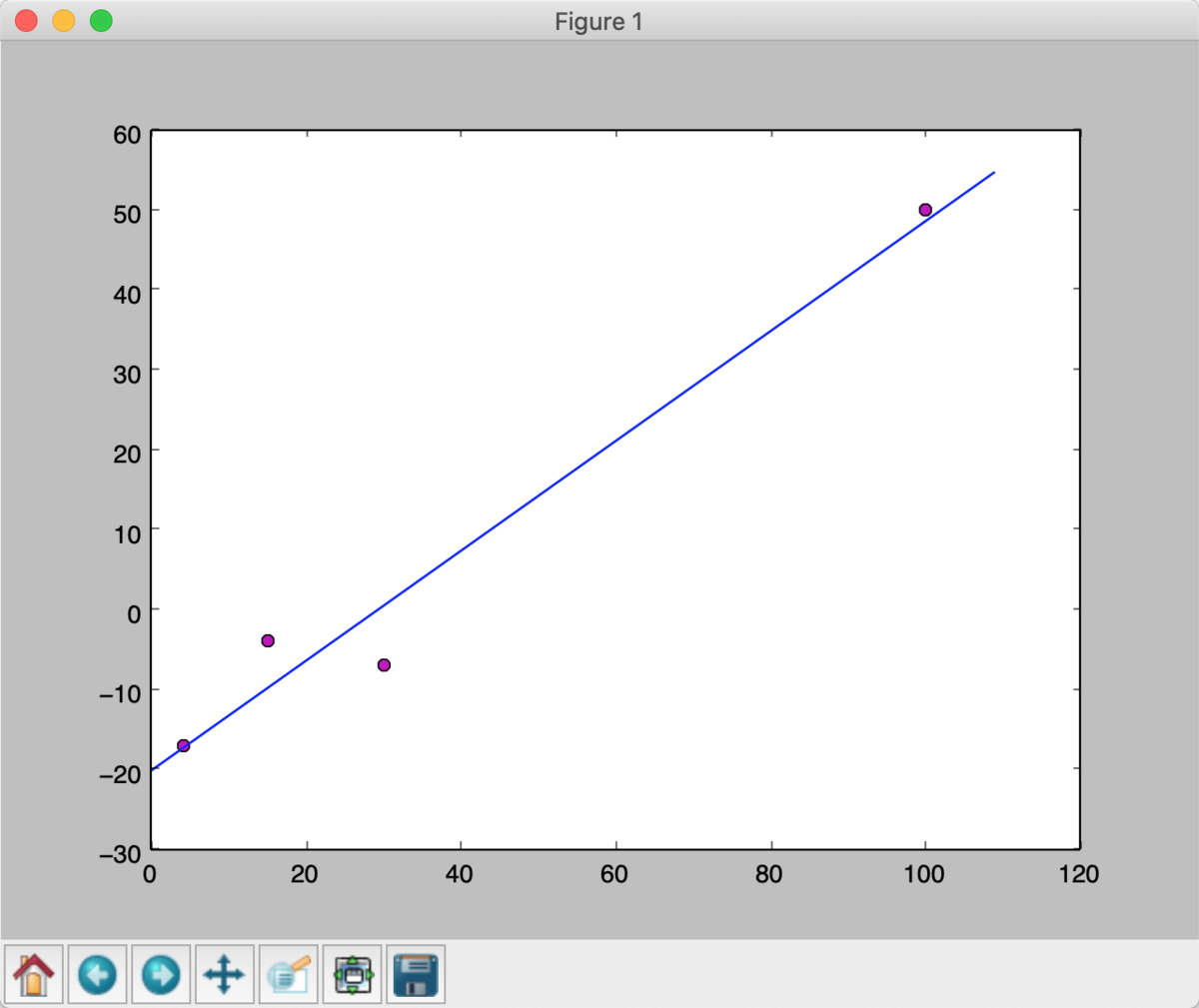
例題

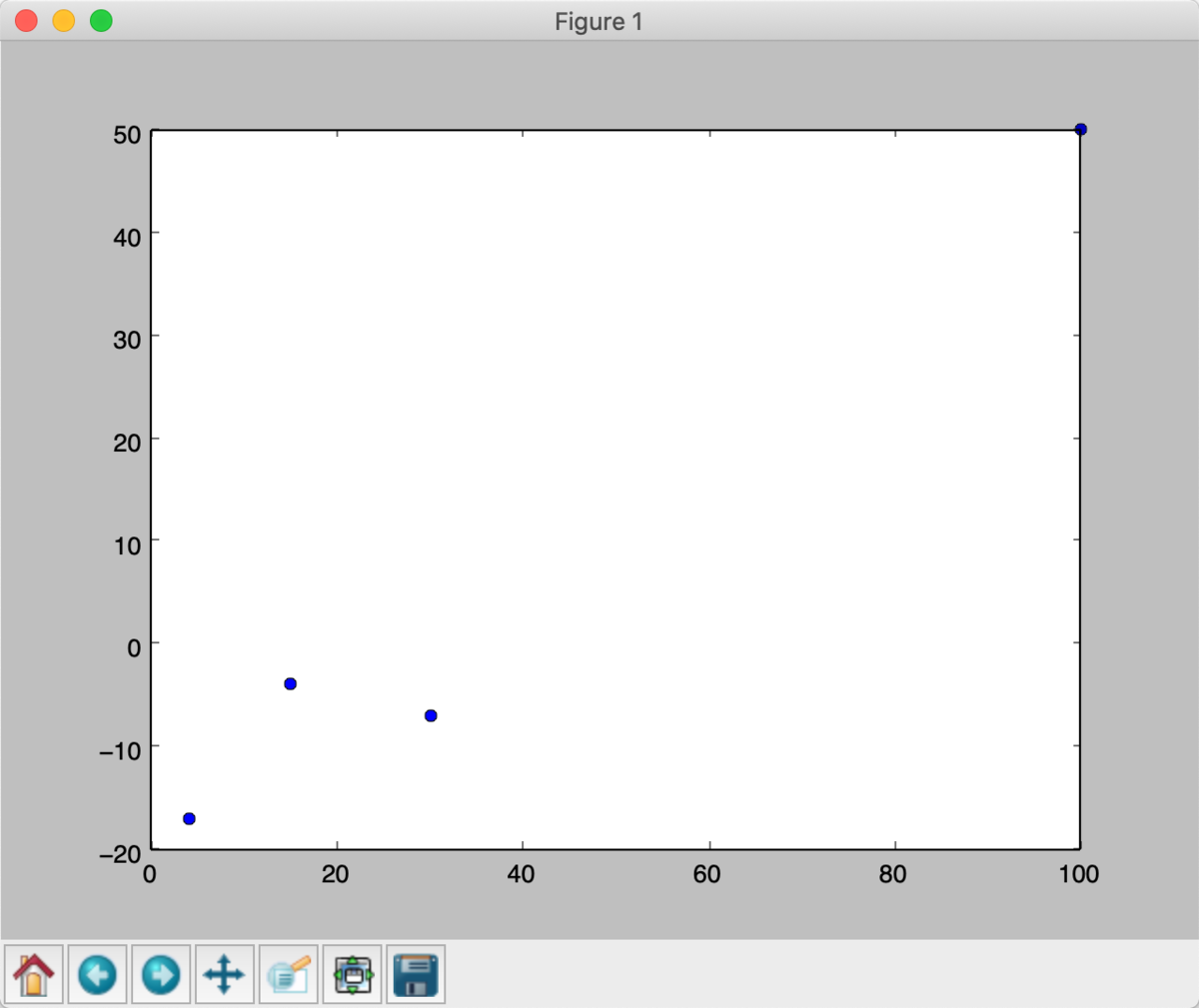
$4$ 点 $\left( 4, \, -17 \right) ,\, \left( 15, \, -4 \right),\, \left( 30, \, -7 \right),\, \left( 100, \, 50 \right)$ に直線を当てはめよ。

まず、この4点の位置関係を matplotlib で可視化してみよう。

from pylab import plot, show

x_numbers = [4, 15, 30, 100]
y_numbers = [-17, -4, -7, 50]

plot(x_numbers, y_numbers, 'o')
show()

f:id:tercel_s:20200229210546p:plain:w350

……なんとなく、右斜め上に向かって伸びる直線が引けそうだね。

じゃあ Python で求解しよう。

方程式の係数行列を $A$ 、右辺のベクトルを $B$ とでもしておこう。

${ \underbrace{\begin{pmatrix} \displaystyle\sum_{\alpha = 1}^{N} x_{\alpha}^{2} & \displaystyle\sum_{\alpha = 1}^{N} x_{\alpha } \\ \displaystyle\sum_{\alpha = 1}^{N} x_{\alpha} & \displaystyle\sum_{\alpha = 1}^{N} 1 \end{pmatrix} }_{A} \begin{pmatrix} a \\ b \end{pmatrix} = \underbrace{ \begin{pmatrix} \displaystyle\sum_{\alpha = 1}^{N} x_{\alpha} y_{\alpha} \\ \displaystyle\sum_{\alpha = 1}^{N} y_{\alpha} \end{pmatrix} }_{B} }$

from functools import reduce
import numpy as np
from numpy.linalg import solve

x_numbers = [4, 15, 30, 100]
y_numbers = [-17, -4, -7, 50]

A = reduce(lambda a, b: a + b, \
    [np.matrix([[x ** 2, x], [x, 1]]) for x in x_numbers])

p = np.array([x_numbers, y_numbers]).T
B = reduce(lambda a, b: a + b, \
    [np.matrix([[x[0] * x[1]], [x[1]]]) for x in p])

print(solve(A, B))

実行すると、こんな感じでターミナルに表示されるよ。

matrix([[  0.68729598],
        [-20.10177525]])

えっ…… コード短っ。

これが連立方程式の解？

そうだよ。

$a \fallingdotseq 0.687,\, b \fallingdotseq -20.1$ だね。

求める直線の式は、 $y = 0.687x - 20.1$ か。

じゃあ、線を引いて答え合わせをしてみよう。

f:id:tercel_s:20200229210801p:plain:w350

おー、、なんかいい感じだね。

おまけ: ちょっと気になる Python の話

ところで、 ${A}$ や ${B}$ を計算するコードにけっこうクセがあると思わない？

思う、、

ちょっと分かりやすくするために番号を振ってみたよ。

x_numbers = [4, 15, 30, 100]
A = reduce(lambda a, b: a + b, \  # ❷
    [np.matrix([[x ** 2, x], [x, 1]]) for x in x_numbers]) # ❶

❶ の処理でやっていることは、イメージにするとこんな感じ。

${ \underbrace{\left[ x_{1},\, x_{2},\, \cdots ,\, x_{N} \right]}_{\texttt{x_numbers}} \rightarrow \left[ \begin{pmatrix} x_{1}^{2} & x_{1} \\ x_{1} & 1 \\ \end{pmatrix},\, \begin{pmatrix} x_{2}^{2} & x_{2} \\ x_{2} & 1 \\ \end{pmatrix},\, \cdots ,\, \begin{pmatrix} x_{N}^{2} & x_{N} \\ x_{N} & 1 \\ \end{pmatrix} \right] }$

なるほど、リスト内包表記で、x_numbers の各要素を行列に map してるんだ。

あとは ❷ の reduce によって、各行列の総和を取っている。

行列 $B$ はどう計算してるの？

こっちはちょっとトリッキーだよ。

これも順番に見ていこうか。

x_numbers = [4, 15, 30, 100]
y_numbers = [-17, -4, -7, 50]

p = np.array([x_numbers, y_numbers]).T  # ❸
B = reduce(lambda a, b: a + b, \  # ❺
    [np.matrix([[x[0] * x[1]], [x[1]]]) for x in p])  # ❹

まず ❸ では、 $x_\alpha$ と $y_\alpha$ のペアを作っている。

x_numbers と y_numbers をがっちゃんこして転置したものを変数 p に代入している。

${ \begin{bmatrix} \begin{bmatrix} x_{1} & x_{2} & \cdots & x_{N} \end{bmatrix} , \\ \begin{bmatrix} y_{1} & y_{2} & \cdots & y_{N} \end{bmatrix} ~ \end{bmatrix} \rightarrow \underbrace{ \begin{bmatrix} \begin{bmatrix} x_{1} & y_{1} \end{bmatrix} , \\ \begin{bmatrix} x_{2} & y_{2} \end{bmatrix} , \\ \vdots \\ \begin{bmatrix} x_{N} & y_{N} \end{bmatrix} ~ \end{bmatrix} }_{\texttt{p}} }$

Tは転置の T なのか。

続いて ❹ では、 $B$ の各項 ${\begin{pmatrix} x_{\alpha} y_{\alpha} & y_{\alpha} \end{pmatrix}^{\mathrm{T}} }$ を計算している。

あとはわかるね？

${ \underbrace{ \begin{bmatrix} \begin{bmatrix} x_{1} & y_{1} \end{bmatrix} , \\ \begin{bmatrix} x_{2} & y_{2} \end{bmatrix} , \\ \vdots \\ \begin{bmatrix} x_{N} & y_{N} \end{bmatrix} ~ \end{bmatrix} }_{\texttt{p}} \rightarrow \left[ \begin{pmatrix} x_1 y_1 \\ y_1 \end{pmatrix},\, \begin{pmatrix} x_2 y_2 \\ y_2 \end{pmatrix},\, \cdots ,\, \begin{pmatrix} x_N y_N \\ y_N \end{pmatrix} \right] }$

最後は ❺ の reduce で全項を足し合わせて $B$ が得られるんだね。

というかすごいね、たったこれだけのコードで方程式が解けるなんて……。

そうだね。

まとめとあとがき

今回取り上げた誤差を最小にするアプローチは、けっこういろんなところで目にする話題なので、今後のために覚えておくといいかも。

たとえば？

そうだなぁ…… たとえば今回のお題って、機械学習における回帰モデルそのものなんだ。

$\displaystyle\sum_{\alpha = 1}^{N} \bigl\{ y_{\alpha } - \left( ax_{\alpha } + b \right) \bigr\}^{2}$ には残差平方和というカッコいい名前があって、これを最小化するように定めた直線を回帰直線って呼んだりする。