VBで特異値分解（ができるライブラリをさがそう！）チュートリアル

Visual Basic

問題

というわけで、今日は「Visual Studioの起動から、特異値分解の問題を一つ解くまで」のチュートリアルをノーカット版でお送りしたいと思います。

ただし、「特異値分解」そのものの解説は記事の対象外とします。ごめんなさい。線形代数の教科書を読んでください(＞＜；)

環境

この記事を書くために使用した環境（OSおよび開発環境のバージョン）は、以下通りです*1。

また、記事中でVisual StudioのNuGetパッケージマネージャを使用し、Math.Net Numericsライブラリを導入します（大学や企業などの場合、プロキシの設定が必要かもしれません。くわしくは、所属する大学や企業のネットワーク管理者にご相談ください。僕は知らん）。

やってみる

新規プロジェクトの作成

Visual Studio を起動したら、[ファイル(F)] → [新しいプロジェクト(P)] の順にクリックします。
f:id:tercel_s:20141012190921p:plain

新しいプロジェクト画面が出てきたら、[テンプレート] → [Visual Basic] → [Windows] を選択します。プロジェクトの種類は、簡単のため [コンソールアプリケーション] にしましょう。
プロジェクト名を適当に入れてOKを押すと、新しいプロジェクトができあがります。
f:id:tercel_s:20141012191607p:plain

ここまでは簡単ですね。
f:id:tercel_s:20141012191858p:plain

ライブラリを導入する

一昔前まで、外部ライブラリを導入しようとすると、バイナリファイルを落としてきて、参照パスを設定して……と、いろいろ面倒な作業が必要でした。

実は、Visual Studio 2013には、NuGetというパッケージ管理ツールが入っており、これを使うと面倒な設定なしにライブラリを導入することができます。知らなかった人は覚えて帰ろう！

まず、[ツール(T)] → [ライブラリ パッケージ マネージャ(N)] → [ソリューションの NuGet パッケージの管理...] の順にクリックします。
f:id:tercel_s:20141012192118p:plain

こんな画面が現れるので、右側の検索ボックスにライブラリ名（ここでは 「Math.Net Numerics」）入力します。すると、インストール可能なライブラリが検索結果に表示されるので、[Math.Net Numerics]を選択して[インストール]をクリック。
f:id:tercel_s:20141012192312p:plain

確認ウィンドウが表示されるので、[OK]をクリック。
f:id:tercel_s:20141012192548p:plain

正常に導入されたところ。
f:id:tercel_s:20141012192706p:plain

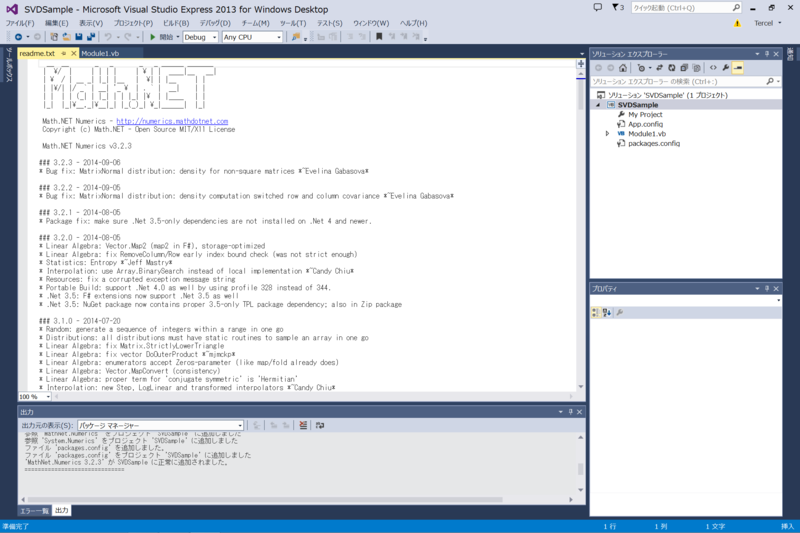
たったこれだけで、ライブラリの導入が終わりました。簡単ですね。

プログラミング

いよいよ、特異値分解（SVD）を行ってみます。

例題

以下の行列 \( \vect{P} \) を特異値分解しましょう。
\[
\vect{P} = \begin{pmatrix}
3 &1 &2 \\
3 &2 &1
\end{pmatrix}
\]

解答例

\[
\vect{P} = \vect{U} \vect{W} \vect{V}^{t} = \underbrace{\begin{pmatrix}
- \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{2}} \\
- \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}
\end{pmatrix}}_{\vect{U}} \underbrace{ \begin{pmatrix}
3 \sqrt{3} & 0 & 0 \\
0 & 1 & 0
\end{pmatrix}}_{\vect{W}} \underbrace{ \begin{pmatrix}
- \frac{2}{\sqrt{6}} & - \frac{1}{\sqrt{6}} & - \frac{1}{\sqrt{6}}\\
0 & \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{2}} \\
- \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}}
\end{pmatrix}}_{\vect{V}^{t}}
\]

VBのコード
Imports MathNet.Numerics.LinearAlgebra
Imports MathNet.Numerics.LinearAlgebra.Double

Module Module1

    Sub Main()
        ' 分解したい行列
        ' [ 3, 1, 2 ]
        ' [ 3, 2, 1 ]
        Dim P As Matrix(Of Double) = DenseMatrix.OfArray(New Double(,) {{3, 1, 2}, {3, 2, 1}})
        Console.Write("P: ")
        Console.WriteLine(P)

        ' SVD 実行
        ' P = U W V^t となるよう P を分解
        Dim svd As Factorization.Svd(Of Double) = P.Svd(True)

        ' 特異ベクトルσを表示
        Console.Write("σ: ")
        Console.WriteLine(svd.S)

        ' U を表示
        Console.Write("U: ")
        Console.WriteLine(svd.U)

        ' W を表示
        Console.Write("W: ")
        Console.WriteLine(svd.W)

        ' V^t を表示
        Console.Write("V^t: ")
        Console.WriteLine(svd.VT)


        ' U W V^t を表示
        ' 元に戻るはず！
        Console.Write("U W V^t (=P): ")
        Console.WriteLine(svd.U.Multiply(svd.W).Multiply(svd.VT))

    End Sub

End Module
実行結果
P: DenseMatrix 2x3-Double
3  1  2
3  2  1

σ: DenseVector 2-Double
5.19615
      1

U: DenseMatrix 2x2-Double
-0.707107  -0.707107
-0.707107   0.707107

W: DenseMatrix 2x3-Double
5.19615  0  0
      0  1  0

V^t: DenseMatrix 3x3-Double
  -0.816497  -0.408248  -0.408248
2.17397E-16   0.707107  -0.707107
   -0.57735    0.57735    0.57735

U W V^t (=P): DenseMatrix 2x3-Double
3  1  2
3  2  1

続行するには何かキーを押してください . . .

f:id:tercel_s:20141012195119p:plain

という感じです、です。

余談

ちなみに、行列のサイズを調べるときには以下のように書きます。

' 行列の行数・列数取得
Console.WriteLine("Pは " & P.RowCount & "行" & P.ColumnCount & "列です")

Pは 2行3列です

特定の要素を取り出したい場合には、indexerを使って配列のように書けます。

Dim row As Integer = 1
Dim col As Integer = 2

' 行列の各要素には、配列のようにアクセスできる
' 要素は0オリジンであることに注意！
Dim element As Double = P(row, col)

Console.WriteLine("Pの" & (row + 1) & "行目, " & (col + 1) & "列目の要素は" & element & "です")

Pの2行目, 3列目の要素は1です

いじょ。

*1:たぶん Windows 7 と Visual Studio 2012でも大丈夫なはず。NuGetを入れさえすれば Visual Studio 2010でもいけると思う。

Copyright (c) 2012 @tercel_s, @iTercel, @pi_cro_s.